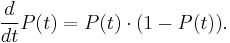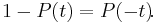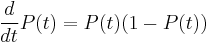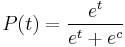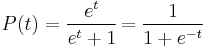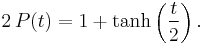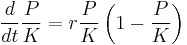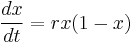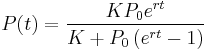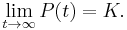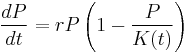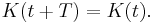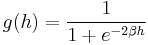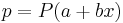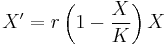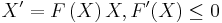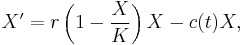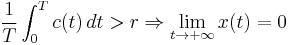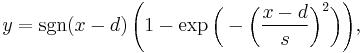Logistic function

For the recurrence relation, see logistic map.

Standard logistic sigmoid function

A logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve (abbreviated S-curve) of growth of some population P. The initial stage of growth is approximately exponential; then, as saturation begins, the growth slows, and at maturity, growth stops.

A simple[1] logistic function may be defined by the formula

P(t) = \frac{1}{1 + e^{-t}} \!

where the variable[2] P might be considered to denote a population and the variable t might be thought of as time[3]. If we now let t range over the real numbers from −∞ to +∞ then we obtain the S-curve shown. In practice, due to the nature of the exponential function e−t, it is sufficient to compute t over a small range of real numbers such as [−6, +6].

The logistic function finds applications in a range of fields, including artificial neural networks, biology, biomathematics, demography, economics, chemistry, mathematical psychology, probability, sociology, political science, and statistics. It has an easily calculated derivative:

\frac{d}{dt}P(t) = P(t)\cdot(1-P(t))\,\! .

The function P has the intuitively appealing quality that

1-P(t) = P(-t)\! .

Contents

Logistic differential equation

The logistic function is the solution of the simple[1] first-order non-linear differential equation

\frac{d}{dt}P(t) = P(t)(1-P(t)) \!

where P is a variable[2] with respect to time t and with boundary condition P(0) = 1/2. This equation is the continuous version of the logistic map. One may readily find the (symbolic) solution to be

P(t)=\frac{e^{t}}{e^{t}+e^{c}}

Choosing the constant of integration 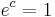e^{c}=1 gives the other well-known form of the definition of the logistic curve

P(t) = \frac{e^{t}}{e^{t} + 1} \! = \frac{1}{1 + e^{-t}} \!

The logistic curve shows early exponential growth for negative t, which slows to linear growth of slope 1/4 near t = 0, then approaches y = 1 with an exponentially decaying gap.

The logistical function is the inverse of the natural logit function and so can be used to convert the logarithm of odds into a probability; the conversion from the log-likelihood ratio of two alternatives also takes the form of a logistic curve.

The logistic sigmoid function is related to the hyperbolic tangent, A.p. by

2 \, P(t) = 1 + \tanh \left( \frac{t}{2} \right).

In ecology: modeling population growth

Pierre-François Verhulst (1804–1849)

A typical application of the logistic equation[4] is a common model of population growth, originally due to Pierre-François Verhulst in 1838, where the rate of reproduction is proportional to:

all else being equal. Thus the second term models the competition for available resources, which tends to limit the population growth. Letting P represent population size (N is often used in ecology instead) and t represent time, this model is formalized by the differential equation:

\frac{dP}{dt}=rP\left(1 - \frac{P}{K}\right)

where the constant r defines the growth rate and K is the carrying capacity.

Interpreting the equation shown above: the early, unimpeded growth rate is modeled by the first term +rP. The value of the rate r represents the proportional increase of the population P in one unit of time. Later, as the population grows, the second term, which multiplied out is −rP2/K, becomes larger than the first as some members of the population P interfere with each other by competing for some critical resource, such as food or living space. This antagonistic effect is called the bottleneck, and is modeled by the value of the parameter K. The competition diminishes the combined growth rate, until the value of P ceases to grow (this is called maturity of the population).

Let us divide both sides of the equation by K[5] to give

\frac{d}{dt}\frac{P}{K}=r\frac{P}{K}\left(1 - \frac{P}{K}\right)

Now setting 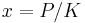x=P/K gives us the differential equation

\frac{dx}{dt} = r x (1-x)

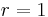For r = 1 we have the particular case with which we started.

In ecology, species are sometimes referred to as r-strategist or K-strategist depending upon the selective processes that have shaped their life history strategies. The solution to the equation (with P_0 being the initial population) is

P(t) = \frac{K P_0 e^{rt}}{K + P_0 \left( e^{rt} - 1\right)}

where

\lim_{t\to\infty} P(t) = K.\,

Which is to say that K is the limiting value of P: the highest value that the population can reach given infinite time (or come close to reaching in finite time). It is important to stress that the carrying capacity is asymptotically reached independently of the initial value P(0) > 0, also in case that P(0) > K.

Time-varying carrying capacity

Since the environmental conditions influences the carrying capacity, as a consequence it can be time-varying: K(t) > 0, leading to the following mathematical model:

\frac{dP}{dt}=rP\left(1 - \frac{P}{K(t)}\right)

A particularly important case is that of carrying capacity that varies periodically with period T:

K(t+T) = K(t).\,

It can be shown that in such a case, independently from the initial value P(0) > 0, P(t) will tend to a unique periodic solution P*(t), whose period is T.

A typical value of T is one year: in such case K(t) reflects periodical variations of weather conditions.

Another interesting generalization is to consider that the carrying capacity K(t) is a function of the population at an earlier time, capturing a delay in the way population modifies its environment. This leads to a logistic delay equation, which has a very rich behavior, with bistability in some parameter range, as well as a monotonic decay to zero, smooth exponential growth, punctuated unlimited growth (i.e., multiple S-shapes), punctuated growth or alternation to a stationary level, oscillatory approach to a stationary level, sustainable oscillations, finite-time singularities as well as finite-time death. <V.I. Yukalov, E.P. Yukalova and D. Sornette, Punctuated Evolution due to Delayed Carrying Capacity, Physica D 238, 1752-1767 (2009)></ref>

In neural networks

Logistic functions are often used in neural networks to introduce nonlinearity in the model and/or to clamp signals to within a specified range. A popular neural net element computes a linear combination of its input signals, and applies a bounded logistic function to the result; this model can be seen as a "smoothed" variant of the classical threshold neuron.

A common choice for the activation or "squashing" functions, used to clip for large magnitudes to keep the response of the neural network bounded[6] is

g(h) = \frac{1}{1 + e^{-2 \beta h}} \!

which we recognize to be of the form of the logistic function. These relationships result in simplified implementations of artificial neural networks with artificial neurons. Practitioners caution that sigmoidal functions which are symmetric about the origin (e.g. the hyperbolic tangent) lead to faster convergence when training networks with backpropagation.[7]

In statistics

Logistic functions are used in several roles in statistics. Firstly, they are the cumulative distribution function of the logistic family of distributions. Secondly they are used in logistic regression to model how the probability p of an event may be affected by one or more explanatory variables: an example would be to have the model

p=P(a + bx)\,

where x is the explanatory variable and a and b are model parameters to be fitted.

An important application of the logistic function is in the Rasch model, used in item response theory. In particular, the Rasch model forms a basis for maximum likelihood estimation of the locations of objects or persons on a continuum, based on collections of categorical data, for example the abilities of persons on a continuum based on responses that have been categorized as correct and incorrect.

In medicine: modeling of growth of tumors

Another application of logistic curve is in medicine, where the logistic differential equation is used to model the growth of tumors. This application can be considered an extension of the above mentioned use in the framework of ecology. Denoting with X(t) the size of the tumor at time t, its dynamics are governed by:

X^{\prime}=r\left(1 - \frac{X}{K}\right)X

which is of the type:

X^{\prime}=F\left(X\right)X, F^{\prime}(X) \le 0

where F(X) is the proliferation rate of the tumor.

If a chemotherapy is started with a log-kill effect, the equation may be revised to be

X^{\prime}=r\left(1 - \frac{X}{K}\right)X - c(t)X,

where c(t) is the therapy-induced death rate. In the idealized case of very long therapy, c(t) can be modeled as a periodic function (of period T) or (in case of continuous infusion therapy) as a constant function, and one has that

\frac{1}{T}\int_{0}^{T}{c(t)\, dt} > r \Rightarrow \lim_{t \rightarrow +\infty }x(t)=0

i.e. if the average therapy-induced death rate is greater than the baseline proliferation rate then there is the eradication of the disease. Of course, this is an over-simplified model of both the growth and the therapy (e.g. it does not take into account the phenomenon of clonal resistance).

In chemistry: reaction models

Concentration of reactants and products in autocatalytical reactions follow the logistic function.

In physics: Fermi distribution

Determines the statistical distribution of fermions over the energy states for a system in thermal equilibrium. In other words, it is the distribution of the probabilities that each possible energy levels is occupied by a fermion, according to Fermi-Dirac statistics.

In linguistics: language change

In linguistics, the logistic function is supposed to model language change[8]. An innovation which is marginal at first begins to spread quickly with time, and by the end of this process there remains only a very small number of items that did not undergo the change in question.

Double logistic function

Double logistic sigmoid curve

The double logistic is a function similar to the logistic function with numerous applications. Its general formula is:

y = \mbox{sgn}(x-d) \, \Bigg(1-\exp\bigg(-\bigg(\frac{x-d}{s}\bigg)^2\bigg)\Bigg),

where d is its centre and s is the steepness factor. Here "sgn" represents the sign function.

It is based on the Gaussian curve and graphically it is similar to two identical logistic sigmoids bonded together at the point x = d.

One of its applications is non-linear normalization of a sample, as it has the property of eliminating outliers.

See also

  • Generalised logistic curve
  • Gompertz curve
  • Hubbert curve
  • Logistic distribution
  • Logistic map
  • Logistic regression
  • Logit
  • Log-likelihood ratio
  • Malthusian growth model
  • r/K selection theory
  • Logistic Smooth-Transmission Model

Notes

  1. ↑ 1.0 1.1 simple: The word simple is used here in a technical sense. There are many different varieties of the form of the logistic function. This is true for most mathematical objects. We will notice the same phenomenon with respect to the corresponding logistic differential equation. It is good practice to begin with a simple form which shows the nature of the mathematical object in question.
  2. ↑ 2.0 2.1 variable: When we speak of the variable P we usually think of it as a function of the variable t which denotes time. Hence, wherever we write P we are using a conventional shorthand for P(t) to say that P varies over time.
  3. ↑ * Verhulst, Pierre-François (1838). "Notice sur la loi que la population poursuit dans son accroissement" (PDF). Correspondance mathématique et physique 10: pp. 113–121. http://books.google.com/books?hl=fr&id=8GsEAAAAYAAJ&jtp=113#v=onepage&q=&f=false. Retrieved 09/08/2009. 
  4. ↑ The Verhulst equation was first published by Pierre-François Verhulst in 1838 after he had read Thomas Malthus' An Essay on the Principle of Population. Verhulst derived his logistic equation to describe the self-limiting growth of a biological population. The equation is also sometimes called the Verhulst-Pearl equation following its rediscovery in 1920. Alfred J. Lotka derived the equation again in 1925, calling it the law of population growth.
  5. ↑ Eric Weisstein at Wolfram Research
  6. ↑ Gershenfeld 1999, p.150
  7. ↑ LeCun, Y.; Bottou, L.; Orr, G.; Muller, K. (1998), Orr, G.; Muller, K., eds., "Efficient BackProp", Neural Networks: Tricks of the trade (Springer), ISBN 3540653112, http://yann.lecun.com/exdb/publis/pdf/lecun-98b.pdf 
  8. ↑ Bod, Hay, Jennedy (eds.) 2003, pp. 147–156

References

  1. Jannedy, Stefanie; Bod, Rens; Hay, Jennifer (2003). Probabilistic Linguistics. Cambridge, Massachusetts: MIT Press. ISBN 0-262-52338-8. 
  2. Gershenfeld, Neil A. (1999). The Nature of Mathematical Modeling. Cambridge, UK: Cambridge University Press. ISBN 978-0521-570954. 
  3. Kingsland, Sharon E. (1995). Modeling nature: episodes in the history of population ecology. Chicago: University of Chicago Press. ISBN 0-226-43728-0. 
  4. Weisstein, Eric W., "Logistic Equation" from MathWorld.

External links